plot.pc

This creates five diagnostic plots:

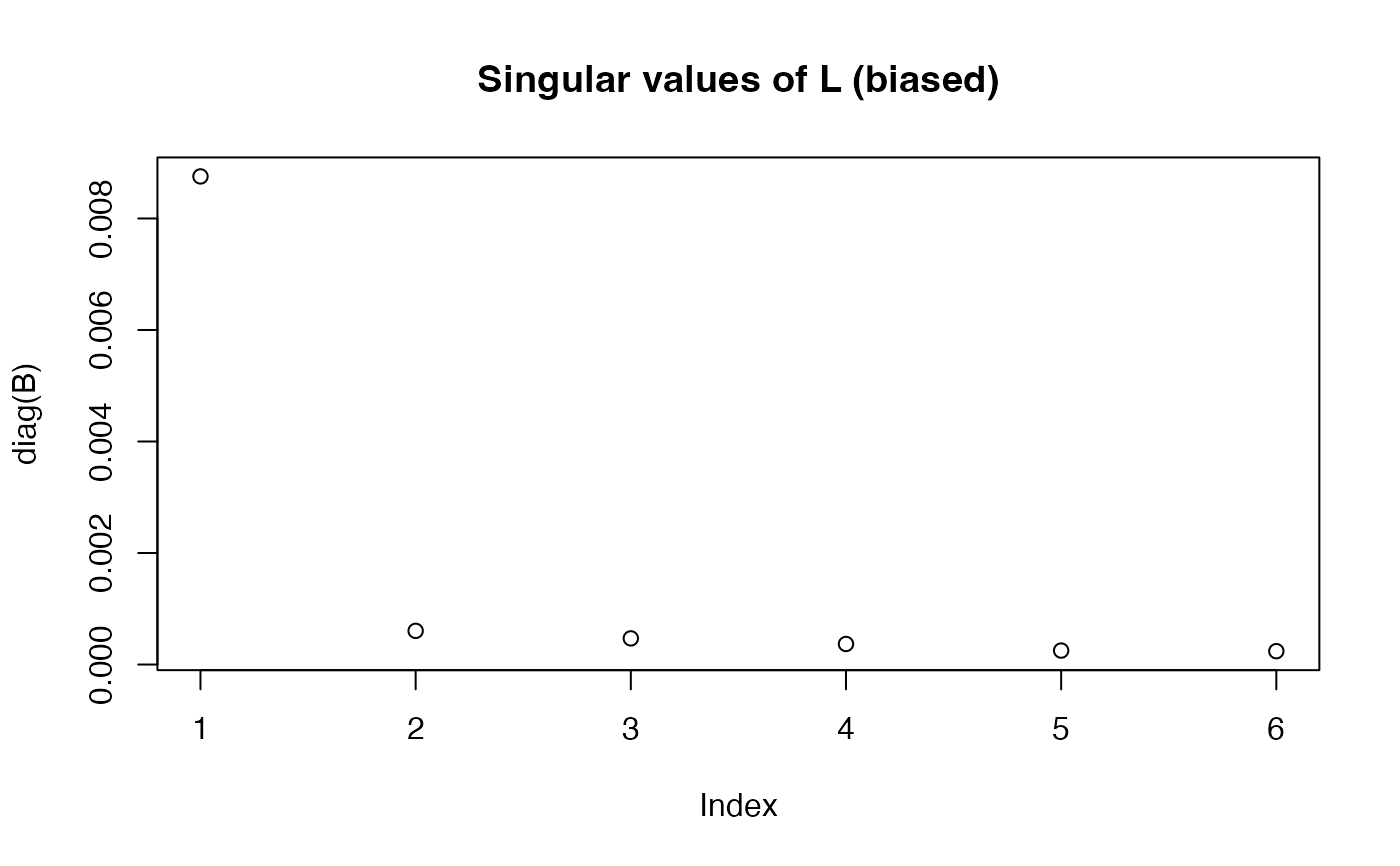
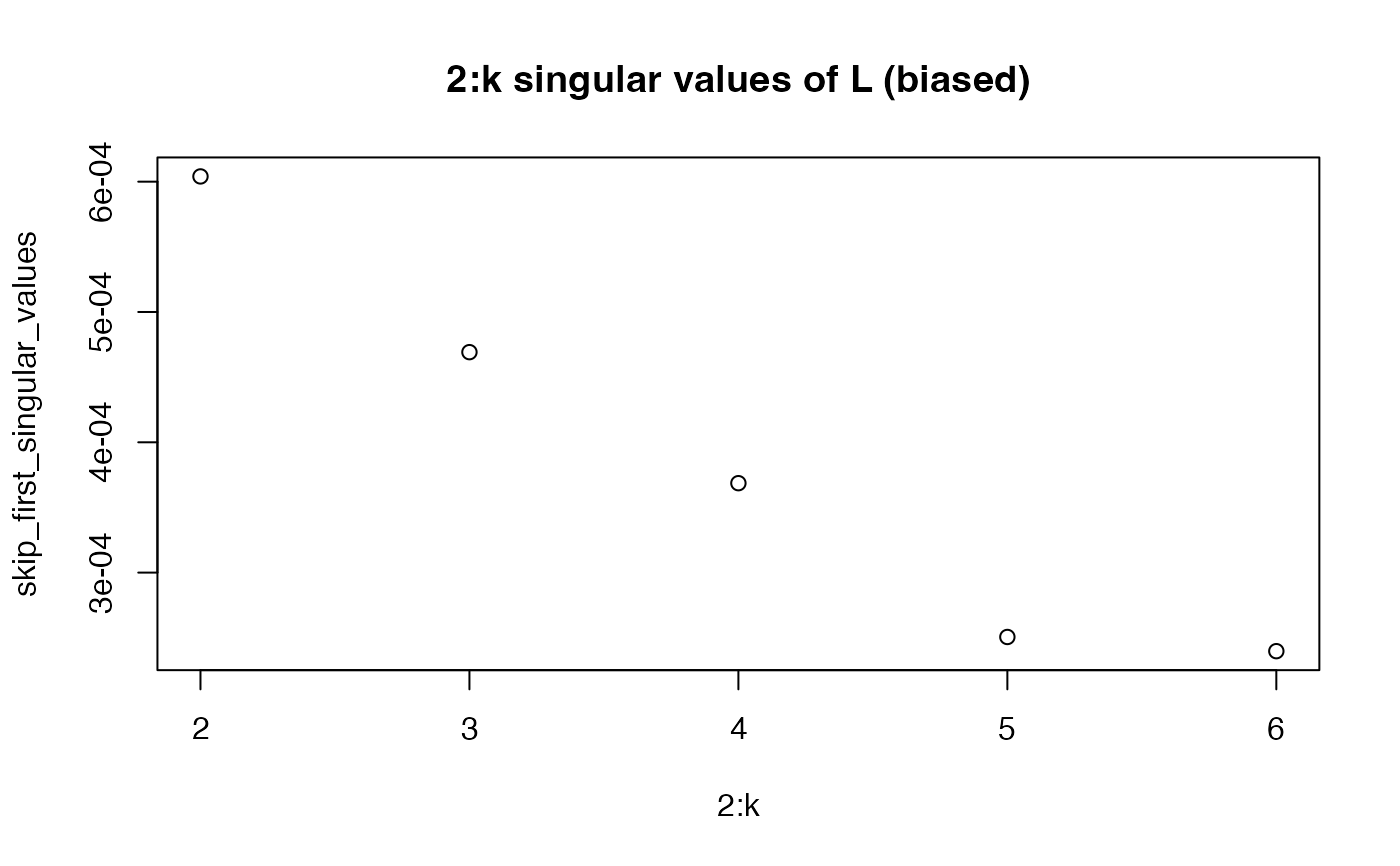
1. Screeplot: The top k singular values of L.

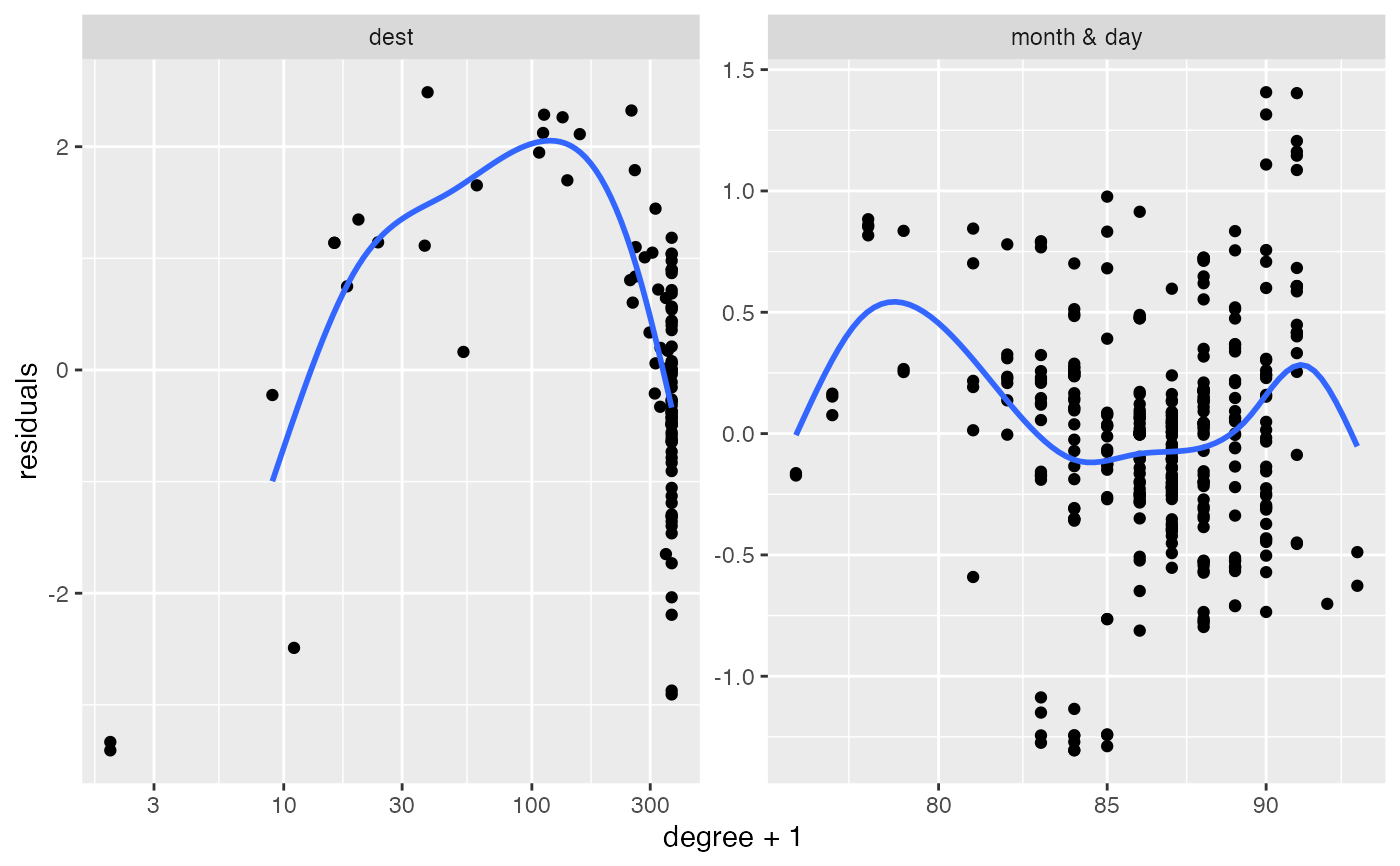
2. Better screeplot: its singular values 2:k (because the first one is usually dominant and difficult to see an elbow past it).

3. A "localization plot" which is very similar (maybe exact?) to this stuff; for each row (and column) compute its degree and its leverage score. Take the log of both. Fit a linear model log(leverage)~log(degree) and plot the residuals against log(degree). If there is localization, I suspect that there will be a big curl on the right side.

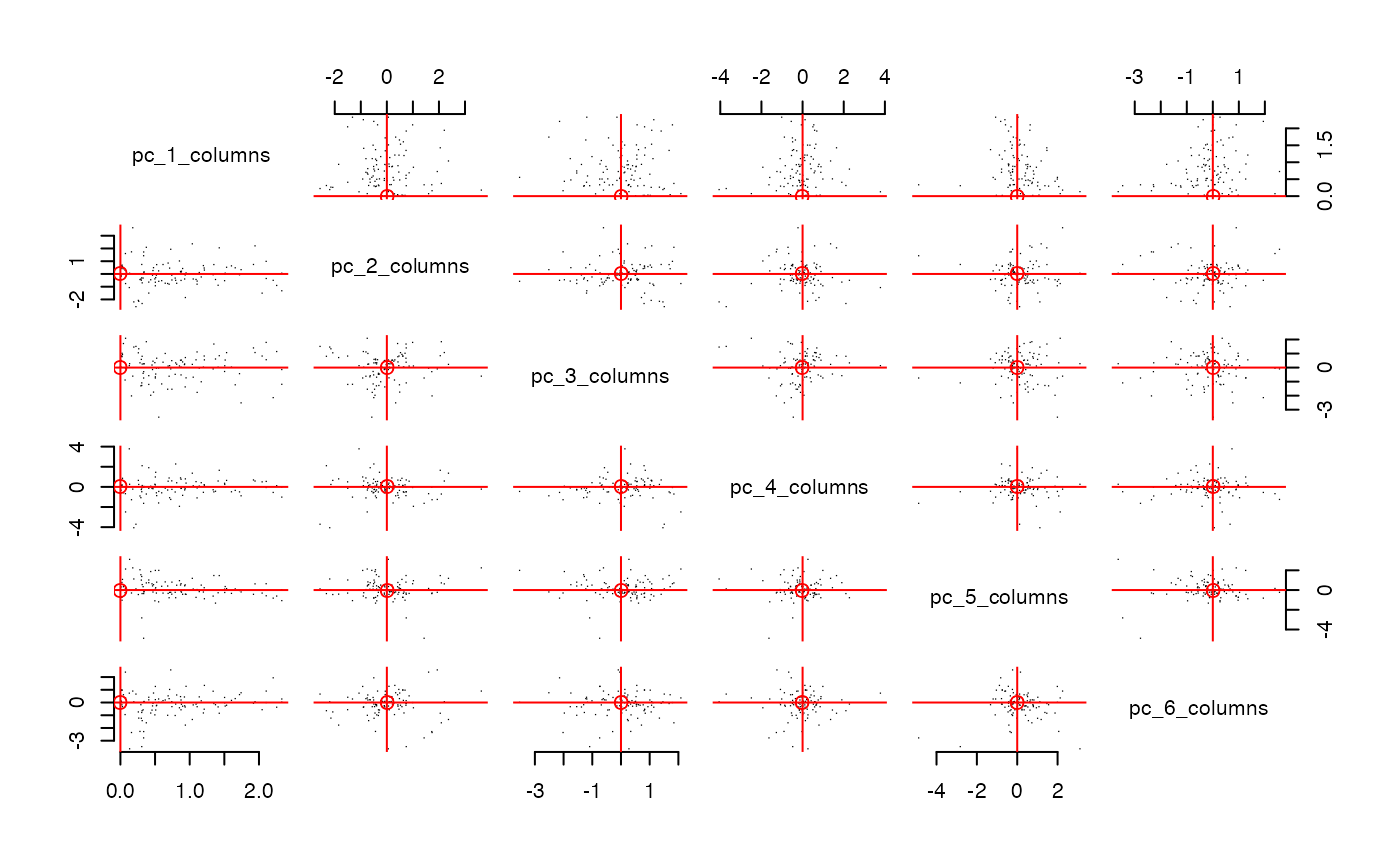
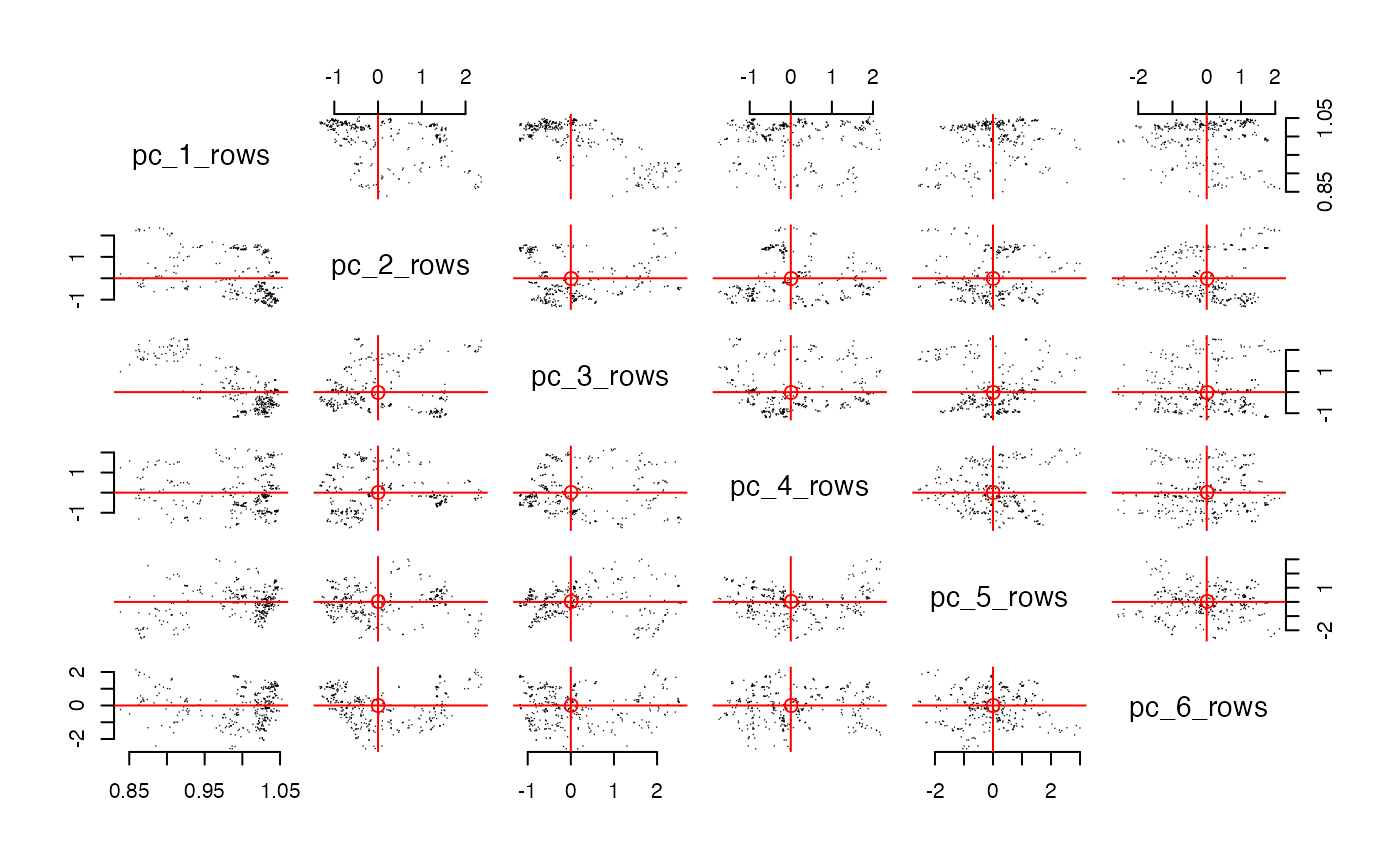
4. Pairs plot of row_features. This is the plot emphasized in the varimax paper. In these example plots below, we do not see very clear radial streaks.

5. A pairs plot for column_features. In both pairs plots, if there are more than 1000 points, then the code samples 1000 points with probability proportional to their leverage scores. It will plot up to k=10 dimensions. If k is larger, then it plots the first 5 and the last 5.

Usage

# S3 method for pc
plot(pcs)

Arguments

pcs

Examples

library(nycflights13)
pcs = pca_count(1 ~ (month & day)*(dest), flights, k = 6)
plot(pcs)

#> Press [Enter] to continue to the next plot...

#> Press [Enter] to continue to the next plot...
#> `geom_smooth()` using formula = 'y ~ s(x, bs = "cs")'

#> Press [Enter] to continue to the next plot...

#> Press [Enter] to continue to the next plot...